十大排序算法总结+工具类
本文共 8964 字,大约阅读时间需要 29 分钟。
十大排序算法总结+工具类
总结
算法重在思想,掌握其思想基本可以将看懂别人写的代码,或能够自己写出来。如果只是使用,每一门编程语言其内部都有其排序算法,在这些算法上进行了优化,效率比这些还要高,使用即可。
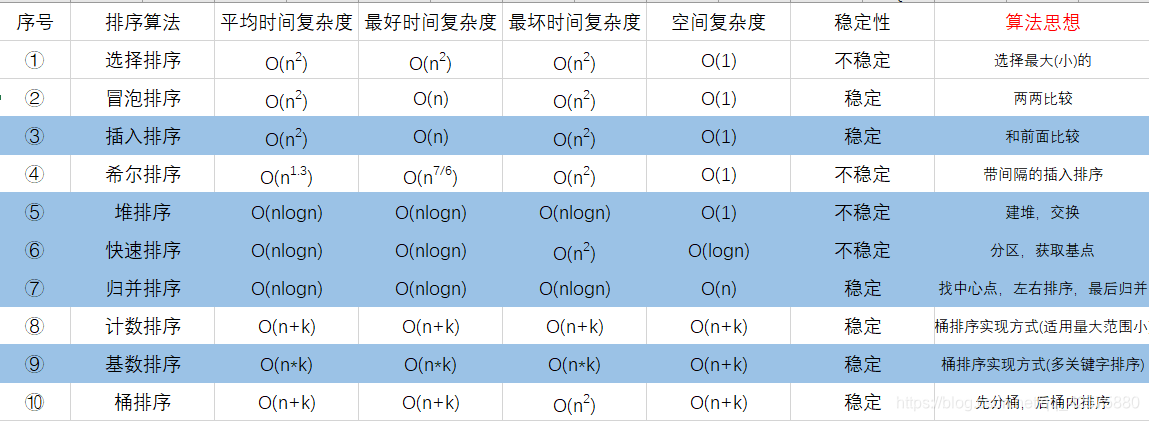
工具类
package com.tmin;import javax.xml.transform.Result;import java.util.*;/** * @author TM * @create 2020-07-16 12:25 */public class SortUtils { /** * 插入排序 * @param arr 数组数据 * @param len 数组长度 */ private static void selectionSort(int[] arr, int len) { for (int i = 0; i < len - 1; i++) { int min = i; for (int j = i + 1; j < len; j++) { if (arr[j] < arr[min]) { min = j; } } swap(arr, i, min); } } /** * 冒泡排序 * @param arr 数组数据 * @param len 数组长度 */ private static void bubbleSort(int[] arr, int len) { for (int i = len - 1; i > 0; i--) { for (int j = 0; j < i; j++) { if (arr[j] > arr[j + 1]) { swap(arr, j, j + 1); } } } } /** * 插入排序 * @param arr 数组数据 * @param len 数组长度 */ private static void insertionSort(int[] arr, int len) { for (int i = 1; i < len; i++) { for (int j = i; j > 0; j--) { if (arr[j] < arr[j - 1]) { swap(arr, j, j - 1); } } } } /** * 希尔排序 * @param arr * @param len */ private static void shellSort(int[] arr, int len) { int h = 1; while (h <= len / 3) { h = h * 3 + 1; } for (int gap = h; gap > 0; gap = (gap - 1) / 3) { for (int i = gap; i < len; i++) { for (int j = i; j > gap - 1; j -= gap) { if (arr[j] < arr[j - gap]) { swap(arr, j, j - gap); } } } } } /** * 堆排序 * @param arr 数组 * @param len 数组长度 */ private static void heapSort(int[] arr, int len) { for (int i = len; i > 0; i--) { //堆化 heapify(arr, i); //交换位置 swap(arr, i - 1, 0); } } /** * 堆化 * @param arr 数组 * @param len 数组长度 */ private static void heapify(int[] arr, int len) { //非叶子结点数len/2 for (int i = len / 2 - 1; i >= 0; i--) { int max = i; if (2 * i + 1 < len && arr[max] < arr[2 * i + 1]) { max = 2 * i + 1; } if (2 * i + 2 < len && arr[max] < arr[2 * i + 2]) { max = 2 * i + 2; } swap(arr, i, max); } } /** * 快速排序 * @param arr 数组数据 * @param left 数组最小索引 * @param right 数组最大索引 */ private static void quickSort(int[] arr, int left, int right) { if (left >= right) { return; } //获取基点 int mid = partition(arr, left, right); //左排序 quickSort(arr, left, mid - 1); //右排序 quickSort(arr, mid + 1, right); } /** * 数组分区 * @param arr 数组数据 * @param left 数组最小索引 * @param right 数组最大索引 * @return 基点 */ private static int partition(int[] arr, int left, int right) { //获取随机索引 int randIndex = new Random().nextInt(right - left + 1); //交换减小获取最大最小值的机率 swap(arr, left + randIndex, right); //获取基准值 int pivot = arr[right]; int leftPtr = left; int rightPtr = right - 1; while (leftPtr <= rightPtr) { while (leftPtr <= rightPtr && arr[leftPtr] <= pivot) { ++leftPtr; } while (leftPtr <= rightPtr && arr[rightPtr] > pivot) { --rightPtr; } if (leftPtr < rightPtr) { swap(arr, leftPtr, rightPtr); } } swap(arr, leftPtr, right); return leftPtr; } /** * 归并排序 * @param arr 数组数据 * @param left 数组最小索引 * @param right 数组最大索引 */ private static void mergeSort(int[] arr, int left, int right) { if (left >= right) { return; } //选取中间点 int mid = left + (right - left) / 2; //左排序 mergeSort(arr, left, mid); //右排序 mergeSort(arr, mid + 1, right); //进行归并 merge(arr, left, mid + 1, right); } /** * 数组大数组分成两个小数组进行归并 * @param arr 数组数据 * @param left 左数组最小索引 * @param right 右数组最小索引 * @param rightBound 右数组最大索引 */ private static void merge(int[] arr, int left, int right, int rightBound) { //创建数组 int[] temp = new int[rightBound - left + 1]; int mid = right - 1; int leftPtr = left; int rightPtr = right; int index = 0; while (leftPtr <= mid && rightPtr <= rightBound) { if (arr[leftPtr] <= arr[rightPtr]) { temp[index++] = arr[leftPtr++]; } else { temp[index++] = arr[rightPtr++]; } } while (leftPtr <= mid) { temp[index++] = arr[leftPtr++]; } while (rightPtr <= rightBound) { temp[index++] = arr[rightPtr++]; } System.arraycopy(temp, 0, arr, left, temp.length); } /** * 计数排序 * @param arr 数组数据 * @param len 数组长度 */ private static void countSort(int[] arr, int len) { int[] count = new int[10]; int[] result = new int[len]; for (int i = 0; i < len; i++) { count[arr[i]]++; } for (int i = 1; i < count.length; i++) { count[i] = count[i] + count[i - 1]; } for (int i = len - 1; i >= 0; i--) { result[--count[arr[i]]] = arr[i]; } System.arraycopy(result, 0, arr, 0, len); } /** * 基数排序 * @param arr 数组数据 * @param len 数组长度 */ private static void radixSort(int[] arr, int len) { //获取最大、最小值 int max = arr[0]; int min = arr[0]; for (int i = 1; i < len; i++) { if (max < arr[i]) { max = arr[i]; } if (min > arr[i]) { min = arr[i]; } } //若存在负数 将所有所有值转换为>=0的数 if (min < 0) { //所有值都加上最小值的绝对值 for (int i = 0; i < len; i++) { arr[i] -= min; } max -= min; } //获取最大值位数 int n = (max + "").length(); //桶数组 int[] count = new int[10]; //临时数组 int[] temp = new int[len]; //依次对数据的个、十、百...位进行排序 for (int i = 0; i < n; i++) { int m = (int) Math.pow(10, i); for (int j = 0; j < len; j++) { //获取数据的每一位 int div = arr[j] / m % 10; //数据入桶 ++count[div]; } //保证数组有序 for (int j = 1; j < count.length; j++) { count[j] += count[j - 1]; } //将数据存入临时数组 for (int k = len - 1; k >= 0; k--) { //获取数据的每一位 int div = arr[k] / m % 10; temp[--count[div]] = arr[k]; } System.arraycopy(temp, 0, arr, 0, len); //将桶中数据个数置零 Arrays.fill(count, 0); } //将数据还原 if (min < 0) { for (int i = 0; i < len; i++) { arr[i] += min; } } } /** * 桶排序 * @param arr 数组 * @param bucketLen 每个桶的长度 */ private static void bucketSort(int[] arr, int bucketLen) { //获取数组中的最大最小值 int min = arr[0]; int max = arr[0]; for (int i = 1; i < arr.length; i++) { if (min > arr[i]) { min = arr[i]; } if (max < arr[i]) { max = arr[i]; } } //根据数据区间以及每个桶中数据的个数 获取需要桶的个数 边界问题 +1 int bucketCount = (max - min) / bucketLen + 1; //对数据进行分桶 List > lists = new ArrayList >(bucketCount); //初始化 for (int i = 0; i < bucketCount; i++) { lists.add(new ArrayList ()); } //将数据分配到桶中 for (int k : arr) { lists.get((k - min) / bucketLen).add(k); } //对每个桶中的数据进行排序 for (int i = 0; i < bucketCount; i++) { Collections.sort(lists.get(i)); } //将桶中的数据复制到原数组 int index = 0; for (int i = 0; i < bucketCount; i++) { for (int j = 0; j < lists.get(i).size(); j++) { arr[index++] = lists.get(i).get(j); } } } private static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } private static void printf(int[] arr) { for (int i : arr) { System.out.print(i + " "); } System.out.println(); }
最后
对于详细注解,可以看下我单独介绍每一种排序算法的文章。
转载地址:http://lobcz.baihongyu.com/
你可能感兴趣的文章
MySQL InnoDB事务隔离级别与锁机制深入解析
查看>>
Mysql InnoDB存储引擎 —— 数据页
查看>>
Mysql InnoDB存储引擎中的checkpoint技术
查看>>
Mysql InnoDB存储引擎中缓冲池Buffer Pool、Redo Log、Bin Log、Undo Log、Channge Buffer
查看>>
MySQL InnoDB引擎的锁机制详解
查看>>
Mysql INNODB引擎行锁的3种算法 Record Lock Next-Key Lock Grap Lock
查看>>
mysql InnoDB数据存储引擎 的B+树索引原理
查看>>
mysql innodb通过使用mvcc来实现可重复读
查看>>
mysql insert update 同时执行_MySQL进阶三板斧(三)看清“触发器 (Trigger)”的真实面目...
查看>>
mysql interval显示条件值_MySQL INTERVAL关键字可以使用哪些不同的单位值?
查看>>
Mysql join原理
查看>>
MySQL Join算法与调优白皮书(二)
查看>>
Mysql order by与limit混用陷阱
查看>>
Mysql order by与limit混用陷阱
查看>>
mysql order by多个字段排序
查看>>
MySQL Order By实现原理分析和Filesort优化
查看>>
mysql problems
查看>>
mysql replace first,MySQL中处理各种重复的一些方法
查看>>
MySQL replace函数替换字符串语句的用法(mysql字符串替换)
查看>>
mysql replace用法
查看>>